Matrix

back
Sections :
  1. #I - A Matrix
  2. #II - Properties
  3. #III - Matrix Methods
Sources :

I - A Matrix :

Definition :

Matrix is a rectangular array of numbers, symbols, points, or characters each belonging to a specific row and column.
Example: \[ \begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \end{bmatrix} \]

2 - Matrix Operations :

both (+) and (-) operation can happen in Matrices on element per element basis.
Example : \[ A = \begin{bmatrix} 1 & 2 \\ 4 & 6 \end{bmatrix} ;B = \begin{bmatrix} 3 & 5 \\ 7 & 9 \end{bmatrix};\] \[A + B = \begin{bmatrix} 4 & 7 \\ 11 & 15 \end{bmatrix} \] - as for (*) operation it requires a more complicated approach, Equation : \[ \begin{bmatrix} a & b \\ c & d \end{bmatrix} × \begin{bmatrix} i & j \\ k & l \end{bmatrix} = \begin{bmatrix} a.i + b.k & a.j + b.l \\ c.i + d.k & c.j + d.l \end{bmatrix} \] Note :

II - Properties :

1 - Types of Matrices :

there are multiple types of matrices each with unique properties,

2 - Determinant of a Matrix :

a determinant is a number associated with a square matrix, symbolized by \(|A|\) or \(det(A)\). it can be used to inverse the matrix if it’s value is none zero.
Equation :

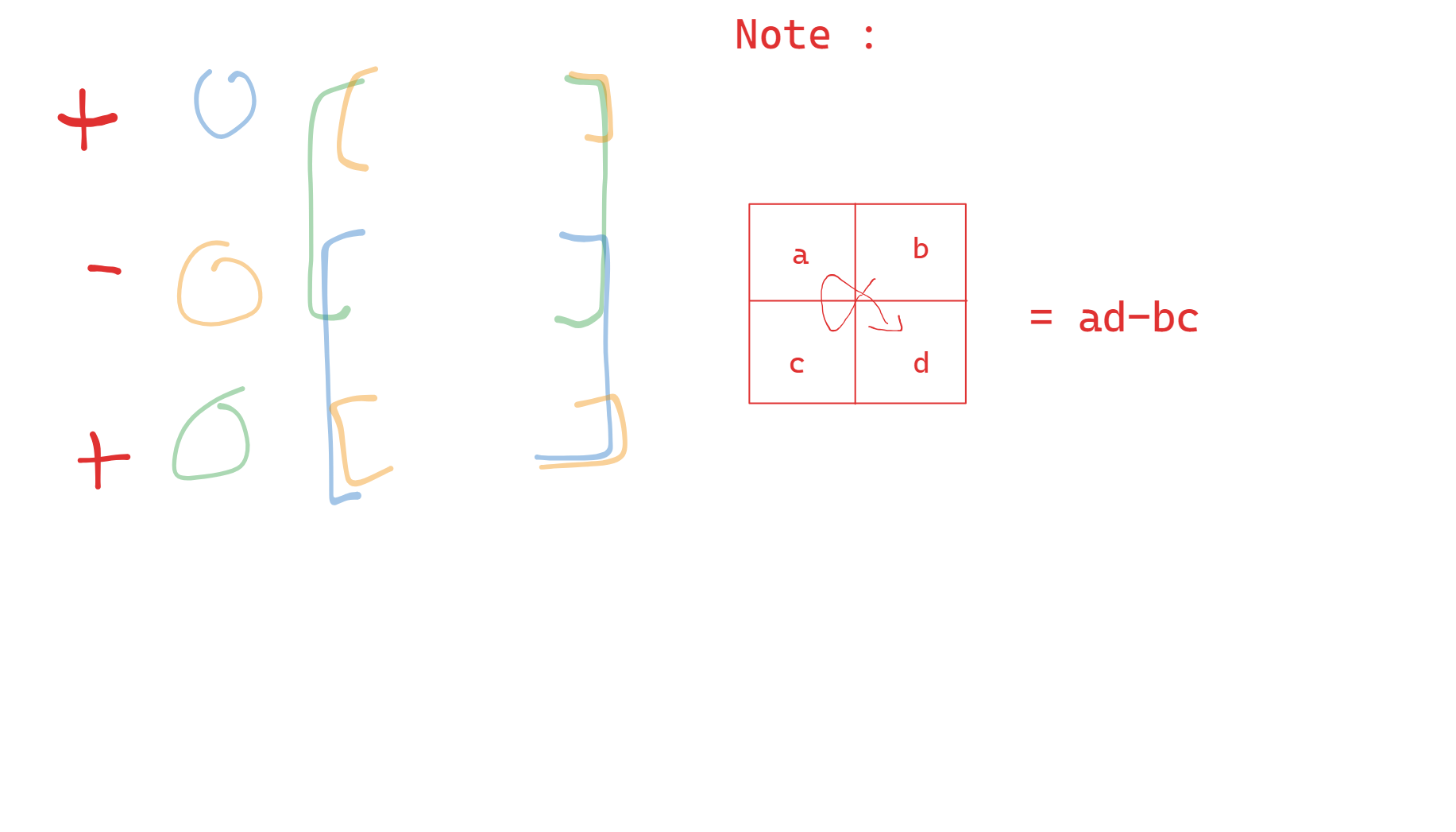\[ A = \begin{bmatrix} a & b & c \\ d & e & f \\ g & h & i \end{bmatrix} \] Matrix determinant.png \[ ⇒ det(A) = a.e.i + b.f.j + d.d.h - c.e.g - b.d.i - a.f.h \] - Note :

the 2x2 matrix used in the multiplication of \(a\) or \(d\) or \(g\) is called the minor of said element, where is Minor of element \(a\) is a 2x2 matrix made by deleting the row and column of the in reference element. it is usually denoted as \(M_{ij}\)

3 - Cofactor of a Matrix :

a cofactor is a property of an element of a matrix, denoted as \(A_{ij}\) or \(C_{ij}\) and is defined as follows : \[C_{ij} = (-1)^{i+j} . M_{ij}\] where is : - \(C_{ij}\) is the cofactor value - \(M_{ij}\) is the minor of element \(a_{ij}\)


Example : for :\[ A = \begin{bmatrix} 5&3&1\\2&0&-1\\1&2&3 \end{bmatrix} \]

the cofactor of \(a_{32}\) would be :

\[ C_{32} = (-1)^{3+2} . \begin{bmatrix} 5&3\\1&2 \end{bmatrix} \] \[ C_{32} = -1 . -7 \] thus \[ C_{32} = 7 \]

4 - adjoint of a Matrix :

a adjoint is a modification of a matrix used to calculate other aspects of said matrix like their inverse. Formula for a 2x2 matrix : for :

\[ A = \begin{bmatrix} a & b \\ c & d \end{bmatrix} \]

we have : \[ adj(A) = \begin{bmatrix} d & -c \\ -b & a \end{bmatrix} \]

Formula for a 3x3 matrix : for : \[ A = \begin{bmatrix} a1&b1&c1\\ a2&b2&c2\\ a3&b3&c3 \end{bmatrix} \] replace each element to it’s respective cofactor \[ A'= \begin{bmatrix} a'1&b'1&c'1\\ a'2&b'2&c'2\\ a'3&b'3&c'3 \end{bmatrix} \] then we just transpose the matrix (which means to flip it) : \[ adj(A) = \begin{bmatrix} a'1&a'2&a'3\\ b'1&b'2&b'3\\ c'1&c'2&c'3 \end{bmatrix} \]

5 - Inverse of a Matrix :

for a matrix \(A\) with a non zero determinant, we can have a inverse matrix of \(A\) called \(A^{-1}\).


a - properties:

- the inverse of \(A\) is \(A^{-1}\) only when : \(A.A^{-1} = A^{-1}.A = In\); - a good indication if a matrix is inversible or not is the determinant, if \(det(A) != 0\) , but even then a inverse may not exist.

b - calculation :

for \(A\) a Matrix we have \(A^{-1}\) as it’s inverse with the formula :

\[ A^{-1} = {1\over{det(A)}}\times adj(A) \]

III - Solving a Matrix :

a matrix may have some unknown values, and there are many methods to solving for these variables. some exceptionell cases need to be known to handle these methods